Аналитика больших данных

Главацкий С.Т., Бурыкин И.Г., Айдагулов Р.Р.

Аннотация курса: Map-Reduce как инструмент для создания параллельных алгоритмов, эффективных для больших объемов данных; обработка наборов документов, поиск по сходству, методы ключевого хеширования (minhashing) и локально чувствительного хеширования; алгоритмы кластеризации многомерных массивов данных; методы поддержки систем принятия решений (recommendation systems); предложенный Google алгоритм определения значимости веб-страниц PageRank; методы понижения размерности массивов данных.

Тематическое содержание курса
1 семестр
Аналитика больших данных: основные алгоритмы
  1. Введение в DataMining.
  2. Технология MapReduce распараллеливания вычислений.
  3. Алгоритмы, использующие MapReduce.
  4. Операции реляционной алгебры. Матричные вычисления.
  5. Алгоритмы обнаружения схожих элементов. Сходство по Жаккару.
  6. Сходство по Жаккару. Методы сжатия больших файлов.
  7. Хеширование, подписи больших файлов.
  8. Локально-чувствительное хеширование документов.
  9. Техника группировок. Построение семейств функций.
  10. Метрики на пространствах данных.
  11. Локально-чувствительные семейства функций хеширования.
  12. Методы высоких степеней сходства. Индексация.
  13. Методы высоких степеней сходства. Использование позиции и длины.
  14. Методы кластеризации в обработке больших данных.
  15. Кластеризация в различных метрических пространствах.
  16. In-Memory базы данных как технологическая платформа для обработки больших данных.
  17. Алгоритмы In-Memory.
2 семестр
Аналитика больших данных: дополнительные главы
  1. Анализ ссылок в Интернет.
  2. Вычисление PageRank.
  3. Модифицированные алгоритмы вычисления PageRank.
  4. Базы данных NoSQL как технологическая платформа для обработки больших данных.
  5. Управление бизнес-процессами.
  6. Интеллектуальный анализ процессов.
  7. Алгоритмы анализа процессов.
  8. Анализ данных с помощью интеллектуального анализа процессов.
  9. Анализ данных (продолжение).
  10. Анализ данных (завершение).
  11. Моделирование и анализ процессов.
  12. Сети Петри.
  13. Сети Петри (продолжение).
  14. Методы обнаружения бизнес-процессов.
  15. Альфа-алгоритм.
  16. Эвристические алгоритмы обнаружения бизнес-процессов.
  17. Эвристические алгоритмы обнаружения бизнес-процессов (продолжение).
Типовые контрольные задания

Задача 1: Универсальное множество U содержит n элементов. Случайным образом выбираются подмножества S и T, содержащие m элементов каждое. Каково ожидаемое значение коэффициента сходства по Жаккару этих множеств?

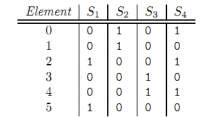
Задача 2: Дана характеристическая матрица множества S1, S2, S3 и S4.

a. вычислите матрицу подписей, используя следующие три хеш-функции : h1(x) = 2x + 1 (mod 6); h2(x) = 3x + 2 (mod 6); h3(x) = 5x + 2 (mod 6).

b. какие из этих функция являются реальными перестановками строк характеристической матрицы?

c. насколько близка оценка сходства по Жаккару этих множеств (с помощью вычисленных подписей) к его истинному значению?

Задача 3: На пространстве неотрицательных чисел какие их следующих функций задают метрику (доказать справедливость, либо привести пример нарушения свойств).

a. max(x, y);

b. diff(x, y) = |x − y|;

c. sum(x, y) = x + y.

Задача 4: Докажите, что расстояние по косинусу между двумя векторами (одной длины), чьи компоненты принимают значения 0 или 1, составляет не более 90º.

Задача 5: Пусть эскизы вычисляются следующим набором «случайных» векторов:

v1 = [+1,+1,+1,−1], v2 = [+1,+1,−1,+1], v3 = [+1,−1,+1,+1] и v4 = [−1,+1,+1,+1].

Вычислите эскизы следующих векторов:

a. [2, 3, 4, 5].

b. [−2, 3,−4, 5].

c. [2,−3, 4,−5].

Для каждой из пар этих трех векторов какова оценка расстояния по косинусу и каково его истинное значение?

Задача 6: Есть 100 корзин, пронумерованных числами 1,2, …, 100, и 100 элементов, также являющихся числами от 1 до 100. Элемент i находится в корзине j тогда и только тогда, когда i делит j без остатка. Например, корзина 24 – это набор элементов {1,2,3,4,6,8,12,24}. Опишите все ассоциативные правила, имеющие достоверность (confidence) = 100%. Какие из следующих правил имеют 100% достоверность (confidence)?

– {4,6} → 24;

– {8} → 16;

– {3,4,5} → 42;

– {8,10} → 20.

Задача 7: Пусть {A,B,C} – часто встречающийся набор элементов, а {B,C,D,E} – не часто встречающийся набор элементов. Верны ли следующие утверждения:

– {B,C,E} – не часто встречающийся набор элементов.

– {B,C} – часто встречающийся набор элементов.

– {A,B,C,D,E,F} может быть как часто встречающимся набором элементов, так и не часто встречающимся набором элементов.

– {B,C,F} – не часто встречающийся набор элементов.

2 семестр

Задача 1: Рассмотрим вершину в дереве решений с 80 экземплярами типа A и 70 экземплярами типа B. Вычислить энтропию данной вершины.

Задача 2: В сети Петри на рисунке (прилагается) найти достижимую маркировку, из которой никакой переход невозможен.

Задача 3: Дан журнал событий L (прилагается). С помощью альфа-алгоритма нарисуйте сеть Петри, соответствующую журналу L.

Задача 4: Рассмотрим журнал событий L (прилагается). Постройте матрицу следа и найдите коэффициент подтверждения на основе матрицы следа).

Задача 5: Рассмотрим модель процесса РN  (прилагается) и след < a,b,c,h,i >. Найти коэффициент подтверждения на основе выравнивания для этого следа, предполагая, что стоимость переходов для всех активностей равна 1.

Перечень учебной литературы